Practice Quantitative Aptitude for CET 2021 with PDF, Number Series, Data Interpretation, Quadratic Equation, Simplification and Approximation, Quadratic Equation , Miscellaneous etc
Hi Aspirants,
In this article we will discuss the questions with solution might be asked in Common Eligibility Test (CET).
In the Budget 2021, Finance Minister — Nirmala Sitharaman — announced to set up a National Recruitment Agency (NRA) to conduct a Common Eligibility Test (CET) for the recruitment of candidates to the Non-Gazetted Posts under RRB/ RRC (Railways), Staff Selection Commission (SSC), and various other Government Exams.
There shall be common registration of candidates through an online portal. To begin with, separate CETs shall be conducted for graduate, higher secondary (class 12-pass) and matriculate (class 10-pass) candidates for non-technical posts, for which recruitment is currently carried through the SSC, the Railway Recruitment Boards (RRBs) and the Institute of Banking Personnel Selection (IBPS).
The score obtained by the candidates in the CET will be made available to him as well as to the individual recruitment agency. The score will be valid for a period of three years from the date of declaration of result.
So we at Smartkeeda help you to reach your Common Eligibility Test Exam by providing strategies and important questions with solution to minimize any losses in CET 2021. Here is an detailed topic of Quantitative Aptitude syllabus and selected important questions for practice which can be asked in CET Exam 2021.
Let’s start to understand each and every topic with detailed Explanation of each and every topic of Quantitative Aptitude for Common Eligibility Test Exam 2021.
The Common Eligibility Test syllabus for Quantitative Aptitude is described as below:
- Number Series
- Data Interpretation
- Simplification/Approximation
- Quadratic Equations
- Miscellaneous
Number Series for CET (Common Eligibility Test):
Basically number series are of two types, one is “Finding the next term” or you can say “Missing term Number Series” and other one is to “Find the Wrong Term”. But we will discuss both “Missing term Series” and “Wrong Term Number Series” in examples as you know that in CET, Missing term Series and Wrong Term Series have high chances to appear.
If you are worrying about "What is Missing Number Series?", So in a simple word we can just say it is a proper sequence of numbers to form out missing numbers. If you didn't understand yet, you will get to know with the help of examples easily.
In the questions of Number Series we have to find out the pattern which help us find the missing term in the series as you can see below:
| Series Pattern | Given Series | |
| 2 | 2 | |
| 2 × 1 + 6 | 8 | |
| 8 × 2 + 12 | 28 | |
| 28 × 3 + 18 | 102 | |
| 102 × 4 + 24 | 432 | |
| 432 × 5 + 30 | 2190 |
| Series Pattern | Given Series | |
| 6 | 6 | |
| 6 × 3 – 2 | 16 | |
| 16 × 3 – 4 | 44 | |
| 44 × 3 – 6 | 126 | |
| 126 × 3 – 8 | 370 | |
| 370 × 3 – 10 | 1100 |
| Series Pattern | Given Series | |
| 51 | 51 | |
| 51 + (52 + 12) = 77 | 77 | |
| 77 + (72 + 72) = 175 | 175 | |
| 175 + (12 + 72 + 52) = 250 | 250 | |
| 250 + (22 + 52 + 02) = 279 | 279 | |
| 279 + (22 + 72 + 92) = 413 | 413 |
| Series Pattern | Given Series | |
| 2 | 2 | |
| 2 × 0.5 + 1 | 2 | |
| 2 × 1.5 + 2 | 5 | |
| 5 × 2.5 + 3 | 15.5 | |
| 15.5 × 3.5 + 4 | 58.25 | |
| 58.25 × 4.5 + 5 | 267.125 |
Ans. D
| Series Pattern | Given Series | |
| 219 | 219 | |
| 219 + (22) = 223 | 223 | |
| 223 + (32) = 232 | 232 | |
| 232 + (42) = 248 | 248 | |
| 248 + (52) = 273 | 273 |
On the other hand we have, "What is Wrong Term Number Series", So in a simple word we can just say it is a proper sequence of numbers to form out wrong pattern (Numbers). If you didn't understand yet, you will get to know with the help of examples easily.
In the questions of Wrong Term Number Series we have to find out the wrong pattern of numbers which help us find the wrong term in the series.
Let discuss Wrong Number Series in detail with the help of examples:
| Series Pattern | Given Series | |
| 21 | 21 | |
| 21 × 1.5 = 31.5 | 31.5 | |
| 31.5 × 2 = 63 | 63 | |
| 63 × 2.5 = 157.5 | 160 | X |
| 157.5 × 3 = 472.5 | 472.5 | |
| 472.5 × 3.5 = 1653.75 | 1653.75 | |
| 1653.75 × 4 = 6615 | 6615 |
| Series Pattern | Given Series | |
| 304 | 304 | |
| 304 + 12 × 1 = 305 | 305 | |
| 305 + 22 × 2 = 313 | 310 | X |
| 313 + 32 × 3 = 340 | 340 | |
| 340 + 42 × 4 = 404 | 404 | |
| 404 + 52 × 5 = 529 | 529 | |
| 529 + 62 × 6 = 745 | 745 |
| Series Pattern | Given Series | |
| 7 | 7 | |
| 7 + 0.5 × 11 = 12.5 | 12.5 | |
| 12.5 + 1.5 × 11 = 29 | 30 | X |
| 29 + 2.5 × 11 = 56.5 | 56.5 | |
| 56.5 + 3.5 × 11 = 95 | 95 | |
| 95 + 4.5 × 11 = 144.5 | 144.5 | |
| 144.5 + 5.5 × 11 = 205 | 205 |
Data Interpretation for CET (Common Eligibility Test):
Data Interpretation or DI can be described as the implementation of some process by which the given data is reviewed for the reason of arriving at an interference. Term Interpreting can described as in which given data requires an analysation to interpretate the information to give the answers of the questions which is asked for Data Interpretation. Generally there are four to five types of formation of DIs like Table Chart, Pie Chart, Line Chart, Caselet DI and Mixed Etc. In Common Eligibility Test, the Data Interpretation you will get one summary with 5 questions as you can see below in the example of Table Chart.
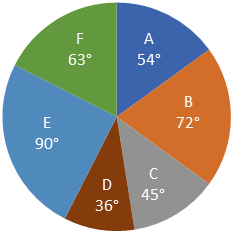
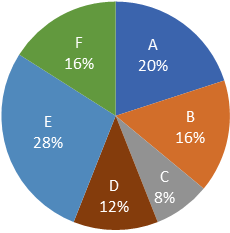
Amount of mined Iron ore = Extracted amount of Iron + Wasted amount of Iron ore.
| = 200 × | 45 | = 25 kg |
| 360 |
Total amount of Iron ore mined by machine E
| = 200 × | 90 | = 50 kg |
| 360 |
Total amount of Iron extracted = (25 + 50) – (2 + 7) = 75 – 9 = 66 kg
Hence, option C is correct.
| = 200 × | 36 | = 20 kg |
| 360 |
Amount of Iron extracted from Iron ore mined by machine D = 20 – 3 = 17 kg
Total wasted amount of Iron ore mined by machine B and F together = 32% of 25 = 8 kg
Required difference = 17 – 8 = 9 kg
Hence, option D is correct.
= (20 + 8)% of 25 = 7 kg
Total amount of Iron ore mined by machine F alone
| = 200 × | 63 | = 35 kg |
| 360 |
| Reqd % = | 7 | × 100 = 20% |
| 35 |
| = 200 × | 72 | = 40 kg |
| 360 |
Total wasted amount of Iron ore mined by machine B = 16% of 25 = 4 kg
Amount of Iron extracted from Iron ore = 40 – 4 = 36 kg
Total cost of Iron extracted from Iron ore by machine B = 36 × 250 = 9000
| Profit % = | 9000 – 8000 | × 100 = 12.5% |
| 8000 |
| = 200 × | 90 | = 50 kg |
| 360 |
Amount of Iron extracted from Iron ore at present = 50 – 7 = 43 kg
Amount of Iron extracted from Iron ore at the end of 2 years from present = 90% of 90% of 43 = 34.83 kg
Total cost of Iron extracted from Iron ore mined by machine E = 34.83 × 200 = Rs.6966
Hence, option C is correct.
Simplification and Approximation for CET (Common Eligibility Test):
Simplification and Approximation is a very easy topic and results in high marks scoring in prelims exams like Common Eligibility Test. To solve such Simplification and Approximation questions, aspirant has to follow VBODMAS rule which stands for Vinculum Bar (-), addition (+), subtraction (–), multiplication (×), division (÷), root (√), and brackets, etc. systematically. Let discuss VBODMAS rule to make this intro clearer.
VBODMAS rule gives the correct order in which various operations regarding simplification are to be performed, so as to find out the values of given expressions in simple ways. Let us see what these letters mean.
V = Vinculum Bar
B = Brackets,
Order of removing brackets
I: Vinculum Brackets (Bar Brackets) ‘–’
II: Small Brackets (Circular Brackets) ‘( )’
III: Middle Brackets (Curly Brackets) ‘{ }’
IV: Square Brackets (Big Brackets) ‘[ ]’
O = Of
D = Division (÷)
M = Multiplication (×)
A = Addition (+)
S = Subtraction (–)
Order of above mentioned operations is as same as the order of letters in the ‘VBODMAS’ from the left to right as
V → B → O → D → M → A → S
Let us understand Simplification and approximation with the help of solved examples:
Quadratic Equation for CET (Common Eligibility Test):
Quadratic Equation is also very easy topic among Common Eligibility Test 2021, you can solve Quadratic Equation questions in just 35 to 55 seconds. Which is quite efficient to save time in your CET Exam. Quadratic Equation can be described as a equation in which the highest exponent on variable is 2. and the writing standard of this equation is ax2 + bx + c=0. So what you need to do in Quadratic Equation you must be given two equations in the form of x and y and you need to find the root values of x and y.
Let discuss Quadratic Equation in detail with the help of examples:
Q.1
I. 18x2 – 33x – 40 = 0
A. if x > y
B. if x ≤ y
C. if x ≥ y
D. if x < y
E. if x = y or relationship between x and y can't be established
Ans. A
From I:
18x2 – 33x – 40 = 0
18x2 – 48x + 15x – 40 = 0
6x(3x – 8) + 5(3x – 8) = 0
(3x – 8)(6x + 5) = 0
| x = | 8 | , – | 5 |
| 3 | 6 |
From II:
12y2 + 47y + 45 = 0
12y2 + 27y + 20y + 45 = 0
3y(4y + 9) + 5(4y + 9) = 0
(4y + 9)(3y + 5) = 0
| y = – | 9 | , – | 5 |
| 4 | 3 |
While comparing the root values of x and y, we find that root values of y are less than the values of x. Hence x > y.
Hence, option A is correct.
Q.2
B. if x ≤ y
C. if x ≥ y
D. if x < y
E. if x = y or relationship between x and y can't be established
Ans. E
18x2 + 73x + 35 = 0
18x2 + 63x + 10x + 35 = 0
9x(2x + 7) + 5(2x + 7) = 0
(2x + 7)(9x + 5) = 0
| x = – | 7 | , – | 5 |
| 2 | 9 |
30y2 + 89y + 63 = 0
30y2 + 35y + 54y + 63 = 0
5y(6y + 7) + 9(6y + 7) = 0
(6y + 7)(5y + 9) = 0
| y = – | 7 | , – | 9 |
| 6 | 5 |
Hence, option E is correct.
Q.3
B. if x ≤ y
C. if x ≥ y
D. if x < y
E. if x = y or relationship between x and y can't be established
Ans. D
x2 + 11x + 30 = 0
Hence, option D is correct.
Q.4
B. if x ≤ y
C. if x ≥ y
D. if x < y
E. if x = y or relationship between x and y can't be established
Ans. E
x2 + 5x – 14 = 0
x2 – 2x + 7x – 14 = 0
Hence, option E is correct.
Q.5
B. if x ≤ y
C. if x ≥ y
D. if x < y
E.if x = y or relationship between x and y can't be established
Ans. E
2x2 – 7x + 6 = 0
2x2 – 3x – 4x + 6 = 0
x(2x – 3) – 2(2x - 3) = 0
(2x – 3)(x – 2) = 0
| x = | 3 | , 2 |
| 2 |
y2 – 5y + 4 = 0
y2 – 4y – y + 4 = 0
y(y – 4) – 1(y – 4) = 0
(y – 4)(y – 1) = 0
y = 4, 1
While comparing the root values of x and y, we find that one root value of y is lies between the values of x. Hence the relationship between x and y can't be established.
Hence, option E is correct.
Miscellaneous for CET (Common Eligibility Test):
Miscellaneous Questions are consist of different topics like time and distance, percentage, probability, boats and stream, average, time and work, problems on numbers, ratio & proportion, permutation and combination etc. In which the important topics such as time and distance, boats and stream, time and work, percentage, profit and loss etc. in which we have given some selected important question to practice to achieve high score in Common Eligibility Test 2021.
P and Q together can do a work in 15/2 days while P and R together can complete the same work in 21/4 days. P works ‘x’ days with B and ‘y’ days with C. If in (x + y) days, double work has been completed, then find the value of ‘x’. [Given (x + y) = 12]
A. 5 days
B. 8 days
C. 4 days
D. 7 days
E. 3 days
Ans. A
Part of work completed by A and B together in one day
| = | 2 |
| 15 |
Part of work completed by A and C together in one day
| = | 4 |
| 21 |
| Therefore, | 2x | + | 4y | = 2 |
| 15 | 21 |
⇒ 7x + 10y = 105 ………..(i)
And, x + y = 12
y = (12 – x) …………..(ii)
Substitute value of (ii) in (i), we get
7x + 10 × (12 – x) = 105
7x + 120 – 10x = 105
3x = 15
x = 5
Hence, option A is correct.
P and Q are two points which are 120 km apart. A boat having speed 25 km/h in still water was going against the stream from point P to point Q. After travelling 80 km, the speed of the stream was increased by 4 km/h due to flood and due to this, the boat had reached point Q 30 minutes later. What was the initial speed of the stream?
A. 4 km/h
B. 3 km/h
C. 5 km/h
D. 6 km/h
E. 2 km/h
Ans. C
Let speed of stream be x km/h
Increased speed of stream = (x + 4) km/h
| So, | { | 80 | + | 40 | } | – | 120 | = | 1 |
| 25 – x | 25 – (x + 4) | 25 – x | 2 |
| ⇒ | 40 | – | 40 | = | 1 |
| 21 – x | 25 – x | 2 |
| ⇒ | 25 – x – 21 + x | = | 1 |
| (21 – x) (25 – x) | 80 |
⇒ 320 = 525 – 46x + x2
⇒ x2 – 46x + 205 = 0
⇒ x2 – 41x – 5x + 205 = 0
⇒ x(x – 41) – 5(x – 41) = 0
⇒ (x – 5)(x – 41) = 0
⇒ x = 5, 41
Since, x ≠ 41
So, x = 5.
Hence, option C is correct.
Preety gave equal amount of money to Sweety and Mousami at simple interest and at compound interest respectively having same rate of interest. After two years, the interest received by Preety from Sweety and Mousami was in the ratio 25:27, respectively. At what rate of interest, the amount of money was given by Preety?
A. 24%
B. 20%
C. 15%
D. 16%
E. 12%
Ans. D
Let principle amount is Rs. p and rate of interest is r%
Amount returned by Sweety to Preety
| = | p × r × 2 | = | pr |
| 100 | 50 |
And, amount returned by Mousami to Preety
| = p × | { | ( | 1 + | r | ) | 2 | – 1 | } |
| 100 |
According to question,
| pr | : p × | { | ( | 1 + | r | ) | 2 | – 1 | } | = 25 : 27 |
| 50 | 100 |
| ⇒ | r | : | { | ( | 1 + | r | ) | 2 | – 1 | } | = 25 : 27 |
| 50 | 100 |
| ⇒ | r | : | ( | r2 | + 1 + | 2r | – 1 | ) | = 25 : 27 |
| 50 | 10000 | 100 |
| ⇒ | r | : | (r2 + 200r) | = 25 : 27 |
| 50 | 10000 |
| ⇒ | r | : | r (r + 200) | = 25 : 27 |
| 50 | 10000 |
| ⇒ 1 : | r + 200 | = 25 : 27 |
| 200 |
| ⇒ | 200 | = | 25 |
| r + 200 | 27 |
⇒ 216 = r + 200
⇒ r = 16
Hence, option D is correct.
One year ago, the ratio of cost price of article A to article B was 10 : 9. The ratio of cost price of last year to present year of both articles A and B are 25 : 29 and 9 : 11, respectively. If the total cost price of both articles in present year is Rs. 113000, then find the present cost price of article B.
A. Rs. 55000
B. Rs. 48000
C. Rs. 42600
D. Rs. 58000
E. None of these
Ans. A
Let cost price of article A and article B one year ago was Rs. 10x and Rs. 9x respectively.
Also, let cost price of article A in last year was Rs. 25y and in present year is Rs. 29y.
So, 25y = 10x
| ⇒ y = | 10x | = | 25x |
| 25 | 5 |
And, let cost price of article B in last year was Rs. 9z and in present year is Rs. 11z.
So, 9z = 9x
⇒ z = x
According to question,
29y + 11z = 113000
| ⇒ 29 × | 2x | + 11x = 113000 |
| 5 |
| ⇒ | 58x + 55x | = 113000 |
| 5 |
⇒ 113x = 113000 × 5
| ⇒ x = | 113000 × 5 |
| 113 |
⇒ x = 5000
Therefore, z = 5000
Present cost price of article B is Rs. 11 × 5000 = Rs. 55000
Hence, option A is correct
The present average age of five members of a family is 32 years. One of the male member of the family get married and age of his wife is 26 years. What will be average age of the family after 6 years if a baby was born after one year of marriage?
A. 32.43 years
B. 28.56 years
C. 29.43 years
D. 37 years
E. 30 years
Ans. A
Average age after marriage
| = | 32 × 5 + 26 | = | 186 | = 31 years |
| 6 | 6 |
Average age of family after 6 years
| = | 186 + 36 + 5 | = | 227 | = 32.43 years |
| 7 | 7 |
Hence, option A is correct
As the notification is released by Government Of India for the Exam of Common Eligibility Test 2021 preparation level of candidates are on highest peak, so if you also want to achieve high marks in this Exam then you will have to practice hard as we all know “practice makes the man perfect”. If you want to boost up your performance in Common Eligibility Test Exam 2021, you can practice more questions in the form of quizzes for Common Eligibility Test 2021 by the links given below .
- Common Eligibility Test Exam 2021 Quiz
- Download Important Questions for CET PDF
- Best online test series for Common Eligibility Test Exam 2021
You can refer to Testzone for competitive exams mock tests of Common Eligibility Test Exam preparation which can help you aspire your dream job by preparing yourself with the best mock test based on day to day updated series.
We hope this article regarding questions for Quantitative Aptitude, with important topics like Number Series, Data Interpretation, Quadratic Equation and Miscellaneous with detailed explanation and solved examples.
At the end we would love to finish this article with a famous quote 'Sooner or Later The Man who Wins is The Man Who Thinks He Can'. So think positive and practice hard and you will definitely achieve your goal "Common Eligibility Test 2021".
Warm Regards,
Team Smartkeeda











