High Level Data Interpretation for IBPS PO | New Pattern Based DI Quiz with PDF
15 Oct 2025

Data interpretation for IBPS PO, Data has to be well organized for it to be useful. This process of interpreting and analysing data to extract meaningful information from it is Data Interpretation. Solving DI problems involves the use of basic formulas and manipulation of numbers.
On this page you will get different types of Data Interpretation which is based on different patterns like given below:
On this page you will get different types of Data Interpretation which is based on different patterns like given below:
- Data Interpretation Based on Time and Distance
- Data Interpretation Based on Profit and Loss
- SI and CI Based Data Interpretation
- Percentage Based Data Interpretation
- Boat and Stream Based Data Interpretation
- Mixed Pattern Based Data Interpretation
Data Interpretation is the most important topic for IBPS PO. It consists of a myriad of graphs, charts and tables form which you have to glean and analyse data. The key to cracking this area is to quickly identify the key pieces of data that you require to work on the questions asked. Here are the DIs Based on differencet maths concept.
- Data Interpretation Based on Time and Distance
Directions : Study the following pie chart and bar chart carefully and answer the questions given below.
A person covers a total distance of 3000 km in 6 days, by bus, by Ola, and by Uber. Study the pie chart and bar graph to answer these questions.
The percentage of total distance travelled in 6 different days.
.png)
The percentage of distance covered by each mode on each day.
.png)
The percentage of distance covered by each mode on each day.
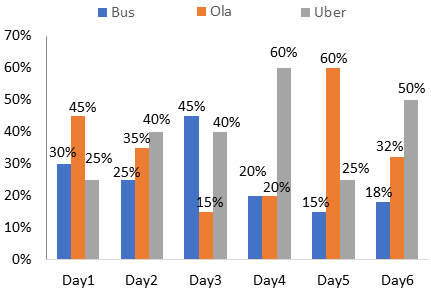
1. What is the total distance covered by Bus?
A. 814.9 km
B. 812.3 km
C. 813.3 km
D. 821.23 km
E. None of these
Explanation :
| Day | Total distance | By bus |
| Day1 | 25% of 3000 = 750 km | 30% of 750 = 225 km |
| Day2 | 15% of 3000 = 450 km | 25% of 450 = 112.5 km |
| Day3 | 20% of 3000 = 600 km | 45% of 600 = 270 km |
| Day4 | 10% of 3000 = 300 km | 20% of 300 = 60 km |
| Day5 | 18% of 3000 = 540 km | 15% of 540 = 81 km |
| Day6 | 12% of 3000 = 360 km | 18% of 360 = 64.8 km |
| Total = 813.3 km |
Hence, option C is correct.
2. If everywhere Ola maintains an average speed of 40 km per hour then what is the total time (In hour) in six days spent on Ola? (approximately)
A. 25 hours
B. 26 hours
C. 27 hours
D. 28 hours
E. 28.5 hours
Explanation :
The total distance travelled by Ola = 1084.2 km
Speed = 40 km per hr
| Time = | 1084.2 | = 27.105 ≈ 27 hrs |
| 40 |
| Day | Total distance | By Ola |
| Day1 | 25% of 3000 = 750 km | 45% of 750 = 337.5 km |
| Day2 | 15% of 3000 = 450 km | 35% of 450 = 157.5 km |
| Day3 | 20% of 3000 = 600 km | 15% of 600 = 90 km |
| Day4 | 10% of 3000 = 300 km | 20% of 300 = 60 km |
| Day5 | 18% of 3000 = 540 km | 60% of 540 = 324 km |
| Day6 | 12% of 3000 = 360 km | 32% of 360 = 115.2 km |
| Total = 1084.2 km |
Hence, option C is correct.
3. The distance travelled by Ola is approximately how much percentage of the distance travelled by Uber? (round off two decimal)
A. 97.21%
B. 102.32%
C. 98.34%
D. 99.91%
E. 106.29%
Explanation :
The total distance travelled by Ola = 1084.2 km
The total distance travelled by Uber = 3000 – 813.3 – 1084.2 = 1102.5 KM
| The reqd. % = | 1084.2 × 100 | = 98.34% |
| 1102.5 |
Hence, option C is correct.
4. Suppose, Instead of Bus, the person uses Ola and the speed of Ola is 25% more than the speed of bus then approximately how many hours the person would save? (The average speed of bus is 30 km per hour)
A. 6.8 hours
B. 7.2 hours
C. 4.6 hours
D. 5.4 hours
E. 4.8 hours
Explanation :
The average speed of bus is 30 km per hour then the average speed of Ola
| = | 30 × 125 | = 37.5 km |
| 100 |
The total distance travelled by bus = 813.3 km
| The reqd. time = | 813.3 | – | 813.3 |
| 30 | 37.5 |
| = 813.3 × | 7.5 | = 5.422 hours |
| 30 × 37.5 |
= 5.4 hours approximately
Hence, option D is correct.
5. Suppose, on the first day, the person travelled for 18 hours and each day he decreases the traveling time by 2 hours then what can be the average speed of the person during the entire period?
| A. 38 | 6 | km per hour |
| 13 |
| B. 37 | 9 | km per hour |
| 13 |
| C. 36 | 2 | km per hour |
| 13 |
| D. 37 | 8 | km per hour |
| 13 |
E. None of these
Explanation :
Total distance = 3000 km
Total time = 18 + 16+ 14 + 12 + 10 + 8 = 78 hours
| The average speed = | total distance |
| total time |
| = | 3000 | = | 500 | = 38 | 6 | km per hour |
| 78 | 13 | 13 |
Hence, option A is correct.
Download free PDF Click Here

- Data Interpretation Based on Profit and Loss
Directions : Study the following table chart carefully and answer the questions given below.
Given table shows the profit/loss, discount and marked up per cent on 6 different electronic articles.
| Articles | Profit % / Loss % | Discount % | Marked up % |
| A.C. | Profit 8% | ---- | 28% |
| Cooler | Loss 8% | ---- | 16% |
| Fridge | ---- | ---- | 15% |
| Oven | ---- | 25% | ---- |
| Geyser | Profit 10% | 8% | ---- |
| Television | ---- | 10% | 12% |
Questions :
1. An owner of the electronics shop sold the cooler to a customer at a loss given in the table. Had he sold it for Rs.475 more, he would have gained a profit of 11%. What is the marked price of the cooler?
A. Rs. 2300
B. Rs. 2500
C. Rs. 2700
D. Rs. 2900
E. None of these
B. Rs. 2500
C. Rs. 2700
D. Rs. 2900
E. None of these
Explanation :
Let the CP of the cooler = 100x
First SP = 92% of 100x = 92x
Second SP = 111% of 100x = 111x = 92x + 475
⇒ 19x = 475
⇒ x = 25
MP of cooler = 116% of 100x = 116x = 116 × 25 = Rs. 2900
Hence, option (D) is correct.
Hence, option (D) is correct.
2. If shopkeeper marked Oven 10% above CP and Geyser 20% above CP and also the CP of Oven is half of the CP of Geyser then find the amount of discount offered by shopkeeper on oven if gained Rs.1000 on selling Geyser?
A. Rs. 1375
B. Rs. 1575
C. Rs. 1480
D. Rs. 1200
E. None of these
B. Rs. 1575
C. Rs. 1480
D. Rs. 1200
E. None of these
Explanation :
Let CP of Geyser = 100x
SP of Geyser = 110% of 100x = 110x
Profit = 110x – 100x = 10x = 1000 (Given)
⇒ x = 100
| CP of oven = | 100x | = 50x |
| 2 |
= 50 × 100 = Rs. 5000
MP of oven = 110% of 5000 = Rs. 5500
Discount on oven = 25% of 5500 = Rs.1375
Hence, option (A) is correct.
Hence, option (A) is correct.
3. The difference between the selling prices of an A.C and a Television is Rs.15400 when Television is sold at a profit of 12%. Cost price of A.C is Rs.15000 more than that of Television. What is the Cost price of A.C.?
A. Rs. 34000
B. Rs. 25000
C. Rs. 35000
D. Rs. 20000
E. None of these
B. Rs. 25000
C. Rs. 35000
D. Rs. 20000
E. None of these
Explanation :
Let CP of AC and Television is ‘100x’ and ‘100y’ respectively.
SP of AC = 108% of 100x = Rs. 108x
SP of Television = 112% of 100x = Rs. 112y
From the question-
⇒ 100x – 100y = 15000 …………. (1)
⇒ 108x – 112y = 15400 …………. (2)
From (1) and (2)-
⇒ x = 350 and y = 200
Cost price of A.C. = 100x = 100 × 350 = Rs.35000
Hence, option (C) is correct.
4. Find the overall profit or loss per cent approximately made by a customer who bought 1 AC set and 1 cooler set. Cost price of 1 AC set is Rs. 30000 and cost price of 1 cooler set is Rs. 5000.
A. 5.71%
B. 2.77%
C. 2.41%
D. 3.24%
E. None of these
Explanation :
B. 2.77%
C. 2.41%
D. 3.24%
E. None of these
Explanation :
Total CP = 30000 + 5000 = Rs.35000
SP of AC = 108% of 30000 = Rs.32400
SP of cooler = 92% of 5000 = Rs.4600
Total SP = 32400 + 4600 = Rs.37000
| Total profit% = | 37000 – 35000 | × 100 ≈ 5.71 |
| 35000 |
Hence, option (A) is correct.
5. Find the total amount paid by a customer after purchasing 1 oven and 1 fridge if the shopkeeper marked the oven up by 15% and he gains 8% on the fridge. Cost price of oven is Rs.15000 and marked price of fridge is Rs.11500.
A. Rs. 13737.5
B. Rs. 23737.5
C. Rs. 22500
D. Rs. 28737.5
E. None of these
B. Rs. 23737.5
C. Rs. 22500
D. Rs. 28737.5
E. None of these
Explanation :
| CP of Fridge = 11500 × | 100 | = Rs. 10000 |
| 115 |
SP of Fridge = 108% of 10000 = Rs.10800
MP of oven = 115% of 15000 = Rs.17250
SP of oven = 75% of 17250 = Rs.12937.5
Total amount paid by customer = SP of Fridge + SP of oven = 10800 + 12937.5 = Rs.23737.5
- SI and CI Based Data Interpretation
The table below shows details about invested by different persons:
| Person | Rate of interest | Time (Years) | Principal (Rs.) | Amount (Rs.) |
| Arun | 6% | 18000 | ||
| Sourav | 6% | 30000 | ||
| Amit | 5 | 29000 | ||
| Piku | 3 | 45000 | ||
| Ankit | 8% | 20000 | ||
| Anita | 2 | 60000 |
All questions are independent from others.
Questions :
1. If the rate of interest received by Arun and Amit is in the ratio of 2 : 3 then find in how many years the money invested by Amit will be doubled with same rate of interest?
A. 14.80
B. 13.45
C. 11.11
D. 15.50
E. 12.54
B. 13.45
C. 11.11
D. 15.50
E. 12.54
Explanation :
| Rate of interest for Amit = | 6 × 3 | = 9% |
| 2 |
Let the principal invested by Amit be Rs. x
So,
| = x + x × 9 × | 5 | = 29000 |
| 100 |
| = 100x + | 45x | = 29000 |
| 100 |
| = 145x = 29000 × | 100 |
| 145 |
= x = 20000
Amount invested by Amit = Rs 20000
To double the invested the time required
Let the time be x
| = 20000 × | 100 | |
| 9 × 20000 |
= 11.11 years.
Hence, option C is correct.
2. If the difference between the interest received by Ankit and Sourav is Rs 4200 and Ankit invested his money for double the time period for which Sourav invested his money then find the amount received by Ankit ?
A. Rs. 30000
B. Rs. 28600
C. Rs. 29600
D. Rs. 35400
E. Rs. 35540
Explanation :
B. Rs. 28600
C. Rs. 29600
D. Rs. 35400
E. Rs. 35540
Explanation :
Let the time for which Sourav invested be x years
So the time for which Ankit invested = 2x years
So, Interest received by Ankit
Interest received by Sourav
So, 3200x – 1800x = 4200
1400x = 4200
x = 3 years
So, Interest received by Ankit
Total amount received by Ankit = Rs. (20000 + 9600) = Rs 29600
Hence, option C is correct.
Interest received by Amit = 29000 – 14500 = Rs 14500
Let the rate of interest for Amit be x
According to question,
= x = 20%
Amount he will if compounded half yearly for 2 years
Hence, option E is correct.
Rate = 10%
Interest for 1st year
Principal for 2nd year= 60000 + 6000 = Rs 66000
Interest for second year
Total interest received by Anita = 6600 + 6000 = Rs 12600
So,
Anita will receive (12600 – 12000) = Rs 600 more interest.
Hence, option A is correct.
5. If the interest received by Anita is Rs 7575 more than interest received by Piku and the rate of interest received by Anita 2% more than the rate of interest received by Arun then find the interest rate received by Piku ?
Explanation :
Let the rate of interest received by Piku be x
According to question,
= 9600 – 1350x = 7575
= 9600 – 7575 = 1350x
= x = 1.5%
Hence, option D is correct.
Download free PDF Click Here
(4).jpg)
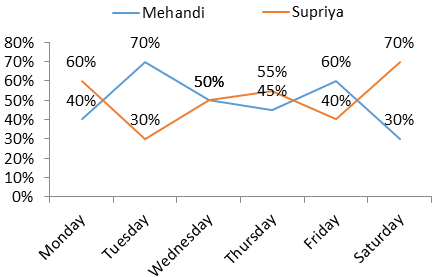
Number of students visiting the chemistry lab on different days
Questions :
Explanation :
Students handled by Mehandi on Thursday and Friday together = 45% of 240 + 60% of 225 = 243
Students handled by Supriya on Thursday = 55% of 240 = 132
Hence, option C is correct.
Explanation :
Students handled by Mehandi on Monday = 40% of 180 = 72 Students handled by Mehandi on Tuesday = 70% of 270 = 189
Students handled by Mehandi on Wednesday = 50% of 150 = 75
Students handled by Mehandi on Thursday = 45% of 240 = 108
Students handled by Mehandi on Friday = 60% of 225 = 135
Students handled by Mehandi on Saturday = 30% of 210 = 63
On Saturday Mehandi handled minimum number of students.
Hence, option D is correct.
Explanation :
Number of students handled by Mehandi on Monday and Tuesday together = 72 + 189 = 261
Number of students handled by Supriya on Wednesday and Friday = 50% of 150 + 40% of 225 = 165
Therefore, respected ratio = 87: 55
Hence, option E is correct.
So the time for which Ankit invested = 2x years
So, Interest received by Ankit
| = 8 × 2x × | 20000 | = Rs. 3200x |
| 100 |
Interest received by Sourav
| = 6 × x × | 30000 | = Rs. 1800x |
| 100 |
So, 3200x – 1800x = 4200
1400x = 4200
x = 3 years
So, Interest received by Ankit
| = 8 × 6 × | 20000 | = Rs. 9600 |
| 100 |
Total amount received by Ankit = Rs. (20000 + 9600) = Rs 29600
Hence, option C is correct.
3. If the amount received by Amit is twice the money invested by him then find amount he will receive after 2 years if he invests the same amount of money in compound interest for 2 years compounded half yearly?
A. Rs. 22199.45
B. Rs. 21992.45
C. Rs. 21292.45
D. Rs. 21929.45
E. Rs. 21229.45
Explanation :
B. Rs. 21992.45
C. Rs. 21292.45
D. Rs. 21929.45
E. Rs. 21229.45
Explanation :
| Amount invested by Amit = | 29000 | = 14500 |
| 2 |
Interest received by Amit = 29000 – 14500 = Rs 14500
Let the rate of interest for Amit be x
According to question,
| = x = | 14500 ×100 | |
| 14500 × 5 |
= x = 20%
Amount he will if compounded half yearly for 2 years
| = 14500 | ( | 1 + | 10 | ) | 4 |
| 100 |
| = 14500 × | 11 | × | 11 | × | 11 | × | 11 | = Rs. 21229.45 | ||
| 10 | 10 | 10 | 10 |
Hence, option E is correct.
4. If the interest received by Anita is 20% of the sum invested by her then find how much more money as interest she would have earned if she had invested the money in compound interest?
A. Rs. 600
B. Rs. 130
C. Rs. 200
D. Rs. 1500
E. Rs. 700
Explanation :
Interest received by Anita
B. Rs. 130
C. Rs. 200
D. Rs. 1500
E. Rs. 700
Explanation :
Interest received by Anita
| = | 20 × 60000 | = Rs. 12000 |
| 100 |
| Rate = 12000 × | 100 | × 60000 |
| 2 |
Rate = 10%
Interest for 1st year
| = 60000 × 10 × | 1 | = Rs. 6000 |
| 100 |
Principal for 2nd year= 60000 + 6000 = Rs 66000
Interest for second year
| = 66000 × 10 × | 1 | = Rs. 6600 |
| 100 |
Total interest received by Anita = 6600 + 6000 = Rs 12600
So,
Anita will receive (12600 – 12000) = Rs 600 more interest.
Hence, option A is correct.
5. If the interest received by Anita is Rs 7575 more than interest received by Piku and the rate of interest received by Anita 2% more than the rate of interest received by Arun then find the interest rate received by Piku ?
A. 8%
B. 1.3%
C. 2.5%
D. 1.5%
E. 1.4%
B. 1.3%
C. 2.5%
D. 1.5%
E. 1.4%
Explanation :
Let the rate of interest received by Piku be x
According to question,
| 60000 × 8 × | 2 | – x × 3 × | 45000 | = 7575 |
| 100 | 100 |
= 9600 – 1350x = 7575
= 9600 – 7575 = 1350x
| = x = | 2025 |
| 1350 |
= x = 1.5%
Hence, option D is correct.
Download free PDF Click Here
(4).jpg)
- Percentage Based Data Interpretation
Direction : Study the following line chart and table chart carefully and answer the questions given below.
Mehandi and Supriya are working in a chemistry laboratory and handled different number of student’s everyday

Number of students visiting the chemistry lab on different days
| Day | Number of students |
| Monday | 180 |
| Tuesday | 270 |
| Wednesday | 150 |
| Thursday | 240 |
| Friday | 225 |
| Saturday | 210 |
Questions :
1. Students handled by Mehandi on Thursday and Friday are what percent of students handle by Supriya on Thursday?
A. 214.67%
B. 192.32%
C. 184.09%
D. 186.56%
E. 134.64%
B. 192.32%
C. 184.09%
D. 186.56%
E. 134.64%
Explanation :
Students handled by Mehandi on Thursday and Friday together = 45% of 240 + 60% of 225 = 243
Students handled by Supriya on Thursday = 55% of 240 = 132
| Therefore, % = | 243 | × 100 = 184.09% |
| 132 |
Hence, option C is correct.
2. On which day of the week Mehandi handled minimum number of students?
A. Wednesday
B. Tuesday
C. Friday
D. Saturday
E. Monday
B. Tuesday
C. Friday
D. Saturday
E. Monday
Explanation :
Students handled by Mehandi on Monday = 40% of 180 = 72 Students handled by Mehandi on Tuesday = 70% of 270 = 189
Students handled by Mehandi on Wednesday = 50% of 150 = 75
Students handled by Mehandi on Thursday = 45% of 240 = 108
Students handled by Mehandi on Friday = 60% of 225 = 135
Students handled by Mehandi on Saturday = 30% of 210 = 63
On Saturday Mehandi handled minimum number of students.
Hence, option D is correct.
3. Find the ratio of the number of students handled by Mehandi on Monday and Tuesday together to number of students handled by Supriya on Wednesday and Friday?
A. 59 : 22
B. 83 : 26
C. 44 : 31
D. 76 : 25
E. 87 : 55
B. 83 : 26
C. 44 : 31
D. 76 : 25
E. 87 : 55
Explanation :
Number of students handled by Mehandi on Monday and Tuesday together = 72 + 189 = 261
Number of students handled by Supriya on Wednesday and Friday = 50% of 150 + 40% of 225 = 165
Therefore, respected ratio = 87: 55
Hence, option E is correct.
4. The number of students handled by Supriya on Monday is what percent of the students handled by her on Tuesday and Saturday together?
A. 48.39%
B. 47.37%
C. 50.41%
D. 42.73%
E. 45.56%
Explanation :
B. 47.37%
C. 50.41%
D. 42.73%
E. 45.56%
Explanation :
Number of students handled by Supriya on Monday = 60% of 180 = 108
Number of students managed by her on Tuesday and Saturday together = 30% of 270 + 70% of 210 = 228
Hence, option B is correct.
Explanation :
Number of students handled by Supriya from Monday to Friday = 486
Number of students handled by Mehandi from Monday to Friday = 579
Hence, option A is correct.
Download free PDF Click Here

.png)
Questions :
1. Find the ratio of the speed of Boats P and Q together in still water to the speed of Boats S and T together in still water.
A. 25 : 32
B. 27 : 19
C. 24 : 39
D. 65 : 48
E. None of these
Explanation :
Ratio = (24 + 24) : (25 + 40)
= 48 : 65
Hence, option E is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
2. If the speed of Boat R in still water is increased by 10% and the speed of stream is increased by 20%, Find the time taken by Boat R to cover the distance of 91 km upstream.
A. 3.5 hours
B. 4 hours
Number of students managed by her on Tuesday and Saturday together = 30% of 270 + 70% of 210 = 228
| Therefore, % = | 108 | × 100 = 47.37% |
| 228 |
Hence, option B is correct.
5. The number of students handled by Supriya from Monday to Friday are what percent of number of students handled by Mehandi from Monday to Friday?
A. 83.94%
B. 78.56%
C. 87.34%
D. 91.34%
E. 88.30%
B. 78.56%
C. 87.34%
D. 91.34%
E. 88.30%
Explanation :
Number of students handled by Mehandi from Monday to Friday = 579
| Therefore, % = | 486 | × 100 = 83.94% |
| 579 |
Hence, option A is correct.
Download free PDF Click Here

- Boat and Stream Based Data Interpretation
Direction: Study the data carefully and answer the question given below :
The table shows the distance travelled by five different boats upstream and downstream in same time and the line chart shows the speed of stream
| Boat | Distance (Upstream) | Distance (Downstream) |
| P | 96 | 288 |
| Q | 120 | 240 |
| R | 100 | 220 |
| S | 150 | 350 |
| T | 180 | 540 |
.png)
Questions :
1. Find the ratio of the speed of Boats P and Q together in still water to the speed of Boats S and T together in still water.
A. 25 : 32
B. 27 : 19
C. 24 : 39
D. 65 : 48
E. None of these
Explanation :
Ratio = (24 + 24) : (25 + 40)
= 48 : 65
Hence, option E is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
| 96 | = | 288 |
| (a – 12) | (a + 12) |
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
| 120 | = | 240 |
| (b – 8) | (b + 8) |
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
| 100 | = | 220 |
| (c – 15) | (c + 15) |
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
| 150 | = | 350 |
| (d – 10) | (d + 10) |
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
| 180 | = | 540 |
| (e – 20) | (e + 20) |
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
2. If the speed of Boat R in still water is increased by 10% and the speed of stream is increased by 20%, Find the time taken by Boat R to cover the distance of 91 km upstream.
A. 3.5 hours
B. 4 hours
C. 6 hours
D. 2.5 hours
E. None of these
Explanation :
Speed of Boat R in still water = 40 × 110% = 44 km/h
Speed of stream = 15 × 120% = 18 km/h
Time taken by Boat R to cover the distance of 91 km upstream = 91/ (44 – 18)
= 91/ 26 = 3.5 hours
Hence, option A is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
3. The distance between point A and point B is 210 km. Boat T travels from point A to B and comes back. What is the time taken by Boat T to cover the total distance.
A. 10 hours
B. 12.5 hours
C. 14 hours
D. 20 hours
E. 8 hours
Explanation :
Speed of Boat P in still water = a km/h
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
4. The ratio of the speeds of the Boat Q to the Boat U in still water is 4 : 5. If the Boat U travels 126 km distance downstream and 81 km distance upstream in 7 hours 30 minutes, What is the speed of stream of Boat U?
A. 15 km/h
B. 10 km/h
C. 20 km/h
D. 12 km/h
E. None of these
Explanation :
Speed of the Boat Q in still water = 24 km/h
Speed of the Boat U in still water
Let the speed of stream = x km/h
According to the question,
2 (3780 – 126x + 2430 + 81x) = 15 (900 – x2)
2 (6210 – 45x) = 13500 – 15x2
12420 – 90x = 13500 – 15x2
15x2 – 90x – 1080 = 0
x2 – 6x – 72 = 0
x2 – 12x + 6x – 72 = 0
x (x – 12) + 6 (x – 12) = 0
(x + 6) (x – 12) = 0
x = –6, 12
Speed of stream = 12 km/h
Hence, option D is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
5. The speed of Boat Q and S in still water together is approximately how much percentage more than the speed of stream of the same boats together?
A. 70%
B. 120%
C. 170%
D. 80%
E. 270%
Explanation :
According to the question,
Speed of Boat Q and S in still water together = (25 + 24) = 49 km/h
Speed of stream of Boat Q and S together = 18 km/h
Hence, option C is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
Download free PDF Click Here

Questions :
Explanation :
Hence, option C is correct.
Explanation :
Hence, option A is correct.
Explanation :
Hence, option D is correct.
Explanation :
Hence, option E is correct.
Download free PDF Click Here
Download High Level Data Interpretation PDF for IBPS PO Click Here.
Download Caselet DI PDF for IBPS PO Pre Click Here.
Problems in High Level Data Interpretation for IBPS PO are probably the closest in resemblance to the kind of problems you will be dealing with regular basis. They test your decision-making ability and speed using the minimum possible data. They help you to draw conclusions from collected data.
D. 2.5 hours
E. None of these
Explanation :
Speed of Boat R in still water = 40 × 110% = 44 km/h
Speed of stream = 15 × 120% = 18 km/h
Time taken by Boat R to cover the distance of 91 km upstream = 91/ (44 – 18)
= 91/ 26 = 3.5 hours
Hence, option A is correct.
Speed of Boat P in still water = a km/h
| 96 | = | 288 |
| (a – 12) | (a + 12) |
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
| 120 | = | 240 |
| (b – 8) | (b + 8) |
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
| 100 | = | 220 |
| (c – 15) | (c + 15) |
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
| 150 | = | 350 |
| (d – 10) | (d + 10) |
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
| 180 | = | 540 |
| (e – 20) | (e + 20) |
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
3. The distance between point A and point B is 210 km. Boat T travels from point A to B and comes back. What is the time taken by Boat T to cover the total distance.
A. 10 hours
B. 12.5 hours
C. 14 hours
D. 20 hours
E. 8 hours
Explanation :
| Total time = | 210 | + | 210 |
| (40 – 20) | (40 + 20) |
| = | 210 | + | 210 |
| 20 | 60 |
= 10.5 + 3.5 = 14 hours
Hence, option C is correct.
Common Explanation:Hence, option C is correct.
Speed of Boat P in still water = a km/h
| 96 | = | 288 |
| (a – 12) | (a + 12) |
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
| 120 | = | 240 |
| (b – 8) | (b + 8) |
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
| 100 | = | 220 |
| (c – 15) | (c + 15) |
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
| 150 | = | 350 |
| (d – 10) | (d + 10) |
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
| 180 | = | 540 |
| (e – 20) | (e + 20) |
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
4. The ratio of the speeds of the Boat Q to the Boat U in still water is 4 : 5. If the Boat U travels 126 km distance downstream and 81 km distance upstream in 7 hours 30 minutes, What is the speed of stream of Boat U?
A. 15 km/h
B. 10 km/h
C. 20 km/h
D. 12 km/h
E. None of these
Explanation :
Speed of the Boat Q in still water = 24 km/h
Speed of the Boat U in still water
| = | 24 | × 5 = 30 km/h |
| 4 |
Let the speed of stream = x km/h
According to the question,
| 126 | + | 81 | = | 15 |
| (30 + x) | (30 – x) | 2 |
| 126 (30 – x) + 81 (30 + x) | = | 15 |
| (900 – x2) | 2 |
2 (3780 – 126x + 2430 + 81x) = 15 (900 – x2)
2 (6210 – 45x) = 13500 – 15x2
12420 – 90x = 13500 – 15x2
15x2 – 90x – 1080 = 0
x2 – 6x – 72 = 0
x2 – 12x + 6x – 72 = 0
x (x – 12) + 6 (x – 12) = 0
(x + 6) (x – 12) = 0
x = –6, 12
Speed of stream = 12 km/h
Hence, option D is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
| 96 | = | 288 |
| (a – 12) | (a + 12) |
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
| 120 | = | 240 |
| (b – 8) | (b + 8) |
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
| 100 | = | 220 |
| (c – 15) | (c + 15) |
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
| 150 | = | 350 |
| (d – 10) | (d + 10) |
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
| 180 | = | 540 |
| (e – 20) | (e + 20) |
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
5. The speed of Boat Q and S in still water together is approximately how much percentage more than the speed of stream of the same boats together?
A. 70%
B. 120%
C. 170%
D. 80%
E. 270%
Explanation :
According to the question,
Speed of Boat Q and S in still water together = (25 + 24) = 49 km/h
Speed of stream of Boat Q and S together = 18 km/h
| % more = | 49 – 18 | × 100 |
| 18 |
| = | 31 | × 100 = 172.22% ≈ 170% |
| 18 |
Hence, option C is correct.
Common Explanation:
Speed of Boat P in still water = a km/h
| 96 | = | 288 |
| (a – 12) | (a + 12) |
96 (a + 12) = 288 (a – 12)
96a + 1152 = 288a – 3456
3456 + 1152 = 288a – 96a
a = 24 km/h
Speed of Boat Q in still water = b km/h
| 120 | = | 240 |
| (b – 8) | (b + 8) |
120 (b + 8) = 240 (b – 8)
120b + 960 = 240b – 1920
1920 + 960 = 240b – 120b
b = 24 km/h
Speed of Boat R in still water = c km/h
| 100 | = | 220 |
| (c – 15) | (c + 15) |
100 (c + 15) = 220 (c – 15)
100c + 1500 = 220c – 3300
3300 + 1500 = 220c – 100c
c = 40 km/h
Speed of Boat S in still water = d km/h
| 150 | = | 350 |
| (d – 10) | (d + 10) |
150 (d + 10) = 350 (d – 10)
150d + 1500 = 350d – 3500
3500 + 1500 = 350d – 150d
d = 25 km/h
Speed of Boat T in still water = e km/h
| 180 | = | 540 |
| (e – 20) | (e + 20) |
180 (e + 20) = 540 (e – 20)
180e + 3600 = 540e – 10800
10800 + 3600 = 540e – 180e
e = 40 km/h
Download free PDF Click Here

- Mixed Pattern Based Data Interpretation
Directions : Study the following web chart carefully and answer the questions given below.
A private tutor has question banks of five subjects (English, Maths, Reasoning, General Awareness, and Computer). The questions are divided into three categories depending on their difficulty level.
.png)
.png)
Questions :
1. The tutor has to make a paper of 60 questions. In how many ways he can choose the questions if 5% questions of the paper are from GA, 45% questions from Maths and at least 28 questions are from reasoning.
A. 2300 × 4060 × 848251
B. 2300 × 4060 × 904801
C. 2300 × 4060 × 906751
D. 2300 × 4060 × 926801
E. 2300 × 4060 × 925001
B. 2300 × 4060 × 904801
C. 2300 × 4060 × 906751
D. 2300 × 4060 × 926801
E. 2300 × 4060 × 925001
Explanation :
Question bank of English contains (5 + 25 + 10) 40 questions
Question bank of Maths contains (7 + 15 + 8) 30 questions
Question bank of GA contains (5 + 6 + 14) 25 questions
Question bank of Computer contains (7 + 6 + 12) 25 questions
Question bank of Reasoning contains (9 + 12 + 9) 30 questions
A paper of 60 questions are to be made that it has 5% questions from GA, 45% of questions from Maths and at least 28 questions from reasoning.
∴ Questions of GA in the paper = 5% of 60 = 3 and Questions of Maths in the paper = 45% of 60 = 27
The different ways that we can choose questions to form such paper are:
i. 3GA × 27Maths × 28reasoning × 2(Computer +English) = 25C3 × 30C27 × 30C28 × 65C2
⇒ 3GA × 27Maths × 28reasoning × 2(Computer +English) = 2300 × 4060 × 435 × 2080
ii. 3GA × 27Maths × 29reasoning × 1(Computer +English) = 25C3 × 30C27 × 30C29 × 65C1
⇒ 3GA × 27Maths × 28reasoning × 1(Computer +English) = 2300 × 4060 × 30 × 65
iii. 3GA × 27Maths × 30reasoning = 25C3 × 30C27 × 30C30
⇒ 3GA × 27Maths × 30reasoning = 2300 × 4060 × 1
∴ Total number of ways in which a paper of 60 questions can be made so that it has 3 GA questions, 27 Maths questions and at least 28 reasoning questions = (2300 × 4060 × 435 × 2080) + (2300 × 4060 × 30 × 65) + (2300 × 4060 × 1)
⇒ Required ways = 2300 × 4060 (435 × 2080 + 30 × 65 + 1)
⇒ Required ways = 2300 × 4060 (904800 + 1950 + 1)
⇒ Required ways = 2300 × 4060 × 906751
Hence, the total number of ways in which a paper of 60 questions can be made so that it has 3 GA questions, 27 Maths questions and at least 28 reasoning questions is 2300 × 4060 × 906751
Hence, option C is correct.
2. A Maths test is to be made using all of the easy and hard level questions only from its question bank. In how many ways the test can be made if no two easy questions are set next to each other?
A. 15120 × 8!
B. 20160 × 9!
C. 2520 × 8!
D. 6720 × 9!
E. 2520 × 7!
Explanation :
∴ Number of ways in which the test can be made if no two easy questions are set next to each other = 8! × 9!/2! = 20160 × 9!
B. 20160 × 9!
C. 2520 × 8!
D. 6720 × 9!
E. 2520 × 7!
Explanation :
Question bank of Maths contains 30 questions.
Out of 30 questions, 7 are easy, 15 are moderate and 8 are hard.
8 hard level questions can be set in 8! Ways
In 8 places of hard questions, there are 9 places in which 7 easy questions are to be set, so that no two easy questions are set to each other
_H1_H2_H3_H4_H5_H6_H7_H8_
⇒ Easy questions can be set in 9P7 ways
| ⇒ Easy questions can be set in | 9! | ways |
| (9 – 7)! |
∴ Number of ways in which the test can be made if no two easy questions are set next to each other = 8! × 9!/2! = 20160 × 9!
Hence, 20160 × 9! Ways in which the test can be made if no two easy questions are set next to each other
Hence, option B is correct.
Hence, option B is correct.
3. A student has to answer 18 questions of reasoning from its question bank, choosing at least 10 from moderate level questions, at least 5 from hard level questions and 1 from easy level, in how many ways can the student answer 18 questions.
A. 31590
B. 30456
C. 27724
D. 32724
E. 28832
B. 30456
C. 27724
D. 32724
E. 28832
Explanation :
Question bank of reasoning contains 30 questions.
Out of 30 questions, 9 are of easy level, 12 are of moderate level and 9 are of hard level questions.
The student has to answer 18 questions.
According to the given information:
Numbers of possibilities are:
i. 12 from moderate level, 5 from hard level and 1 from easy level = 12C12 × 9C5 × 9C1
ii. 10 from moderate level, 7 from hard level and 1 from easy level = 12C10 × 9C7 × 9C1
iii. 11 from moderate level, 6 from hard level and 1 from easy level = 12C11 × 9C6 × 9C1
∴ Required number of ways = (12C12 × 9C5 × 9C1) + (12C10 × 9C7 × 9C1) + (12C11 × 9C6 × 9C1)
⇒ Required number of ways = (1 × 126 × 9) + (66 × 36 × 9) + (12 × 84 × 9)
⇒ Required number of ways = (1134) + (21384) + (9072)
⇒ Required number of ways = 31590
Hence, in 31590 ways a student can answer 18 questions of reasoning from its question bank, choosing at least 10 from moderate level questions, at least 5 from hard level questions and 1 from easy level.
Hence, option A is correct.
4. Find the number of ways in which the tutor can choose questions for an English test of 28 questions which contain 3 easy questions, 23 moderate questions and at most 4 hard questions from its question bank?
A. 30000
B. 69000
C. 75000
D. 135000
E. 360000
B. 69000
C. 75000
D. 135000
E. 360000
Explanation :
Question bank of English contains 40 questions.
Out of 40 questions, 5 are of the easy level, 25 are of moderate level and 10 are of hard level questions.
The tutor has to choose questions for an English test of 28 questions which contain 3 easy questions, 23 moderate questions and at most 4 hard questions
The test can be prepared in following way:
3 easy question, 23 moderate questions, 2 hard question = 5C3 × 25C23 × 10C2
⇒ Number of ways in which the test can be prepared = 10 × 300 × 45
⇒ Number of ways in which the test can be prepared = 135000
Hence, in 135000 ways a tutor can choose questions for an English test of 28 questions which contain 3 easy questions, 23
moderate questions and at most 4 hard questions.
moderate questions and at most 4 hard questions.
Hence, option D is correct.
5. If an entire test paper is created from only easy level questions of the question bank then in how many different ways can the questions be arranged such that all the questions from Maths and reasoning are set together?
A. 30! 17!
B. 17! 16!
C. 18! 17!
D. 33! 16!
E. 18! 16!
B. 17! 16!
C. 18! 17!
D. 33! 16!
E. 18! 16!
Question bank contains 5 easy level English questions, 7 easy level Maths questions, 9 easy level Reasoning questions, 5 easy level G.A questions and 7 easy level computer questions
⇒ There are a total of 33 easy level questions.
But all Maths and Reasoning questions are set next to each other
⇒ 16 questions are grouped and can be considered as 1 question
∴ We can assume a total of (33 – 16 + 1) 18 questions which need to be arranged.
⇒ 18 questions can be arranged in 18! Ways
Now, the number of ways in which Maths and reasoning question can be arranged = 16!
∴ Required number of ways = 18! 16!
Hence, in 18! 16! Ways questions can be arranged if Maths and reasoning questions are always set next to each other.
Hence, option E is correct.
Download free PDF Click Here
Download High Level Data Interpretation PDF for IBPS PO Click Here.
Download Caselet DI PDF for IBPS PO Pre Click Here.
Problems in High Level Data Interpretation for IBPS PO are probably the closest in resemblance to the kind of problems you will be dealing with regular basis. They test your decision-making ability and speed using the minimum possible data. They help you to draw conclusions from collected data.
Smartkeeda always concern about aspirants that’s why they launched Testzone for all Bank and Insurance exams test series at least price.
Take free IBPS PO Pre Mock Test Click Here.
Regards,
Team Smartkeeda









